728x90
반응형
본 블로그의 [T-test] 독립표본과 대응표본의 평균 검정 글에서 T-test의 개념에 대해 다뤄보았다.
이론을 공부했다면 예제 실습을 해 보는 것은 당연한 수순이라 생각한다.
따라서 앞선 이론을 바탕으로
Z-test, One-Sample T-test(단일 표폰 t-test), Independent_Sample T-test(독립표본 t-test), Paired_Sample T-test(대응표본 t-test) 등에 대해 실습해 보자.
실습의 과정과 목표
- Python (Google colab) 사용
- 다시 한번 이론 정리
- 간단한 예제 코드로 분석해 보기
- 그래프 시각화 해보기
이 글의 내용과 예제코드의 출처는 연세 IT미래교육원의 수업 과정 중 정지훈 강사님의 교육을 바탕으로 작성되었습니다.
첫 실습 예제는 제목과 같이 Z-TEST & One-Sample T-TEST에 대한 예제이다.
목차
- 평균의 비교
- One-Sample z-test
- One-Sample z-test 예제 실습
- One-Sample T-test
- One-Sample T-test 예제 실습
- pingouin 라이브러리 소개
1. 평균의 비교
- 일반적으로 t-test를 사용 ( 독립성, 정규성, 등분산성 확인 )
- t-test의 종류
- one sample t-test
- student t-test
- welch's test
- paired sample t-test
- t-test 효과의 표준 척도 : Cohen's D
2. One-Sample z-test
- 가장 쓸모없는 test 중 하나
- 이 test의 유일한 용도는 통계를 가르칠 때 사용
- 전제 조건
- 정규성(Normality) : 실제 모집단은 정규 분포를 따른다.
- 모집단 표준편차 알고 있다 : 모집단의 실제 표준 편차를 알고 있다
- 평균을 모르면 표준편차를 알 수 없다. (평균을 검정하는 건데 평균을 알고 있다???)
- 현실적으로 모집단의 평균과 표준편차를 알 방법이 없기 때문에 쓸모없음.
- 무엇을 검정하는가?
- 추출된 표본이 동일 모집단에 속하는지 가설 검증
- 가설검정
- 귀무가설(H0) : 표본 평균이 모집단의 평균과 같음
- 대립가설(H1) : 표본 평균이 모집단의 평균과 같지 않음
3. One-Sample z-test 예제 실습
- 가정 : 모집단의 평균과 표준편차를 알고 있다.
- 평균 : 67.5
- 표준편차 : 9.5
- 20명 심리학 학생 점수 추출
- '20명의 평균은 67.5와 같은가? 다른가?'를 검정할 것이다.
3-1. 시각화
- 평균이 67.5이고, 표준편차가 9.5인 그래프를 그려본다.
- 이때 모집단의 수는 100개이다.
- 히스토그램은 추출된 20개의 샘플의 분포를 나타낸다.
3-2. 데이터 불러오기 및 샘플의 최대/최소 설정
- 추출된 각각의 데이터는 50~89 사이에서만 나오게 설정하였다.
import pandas as pd
df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/zeppo.csv")
df['grades'].min(), df['grades'].max()
# (50, 89)3-3. 가설 세우기
- 귀무가설(H0) : 추출된 20개의 샘플 데이터의 평균은 67.5이다.
- 대립가설(H1) : H0가 아니다.
# 그래프로 시각화 하기.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import scipy.stats as stats
mu = 67.5 # 평균 67.5 설정
sigma = 9.5 # 표준편차 9.5 설정
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)# 정규분포 그래프 생성, 첨도설정(범위 및 개수)
y = 100* stats.norm.pdf(x, mu, sigma) # Y축 확률밀도함수 설정
# stats.norm.pdf(x, mu, sigma)는 함수는 주어진 값 x에서 정규(가우스) 분포의
# 확률 밀도 함수(PDF)를 계산하며, 평균은 mu이고 표준 편차는 sigma이다.
# 100을 곱한 이유 : x의 범위가 작아서 y값이 작게 나오기 때문
fig, ax = plt.subplots() # 그래프 fig 생성
ax1 = sns.histplot(df['grades'])# 1번 그래프 : grade에 대한 히스토그램
ax2 = sns.lineplot(x=x,y=y, color='black') # 2번 그래프 : x, y 정규분포 선그래프
plt.ylim(bottom=-1) # y축 0 위치 설정 (최소값 설정)
ax1.set_frame_on(False) # 바깥 테두리 삭제
ax1.axes.get_yaxis().set_visible(False) # y축 눈금/레이블 삭제
plt.show()
3-4. 샘플의 평균 구하기
# 샘플의 평균 구하기
import statistics
statistics.mean(df['grades'])
# 72.3- 모집단의 평균은 67.5이고, 추출된 샘플의 평균은 72.3이다.
- 모집단의 평균과 20개의 추출된 평균은 다르다고 볼 수 있는가?
- 우연히 샘플링 에러로 72.3이 나온 것인가?
- 결정을 어떻게 내릴 수 있는가?
3-5. 가설 검정
3-5-1. 가설 검정의 전제조건
- 샘플은 정규분포를 이루고 있다. (정규성(Normality))
- 샘플의 관측값은 서로 독립적으로 생성됨 (독립성(Independence))
- 모집단의 표준편차는 9.5이다.
- stats.norm.pdf(x, mu, sigma)는 함수 : 주어진 값 x에서 정규 분포의 확률 밀도 함수(PDF)를 계산하며, 평균은 mu이고 표준 편차는 sigma이다.
- pdf 함수는 평균과 표준편차가 주어졌을 때 무작위 변수가 특정 값 x를 취할 확률을 반환한다.
- 표준 편차 시그마는 곡선의 확산 또는 폭을 결정한다.
- 요약하면, stats.norm.pdf(x, mu, sigma)는 평균 mu와 표준 편차 시그마가 주어질 때 특정 값 x에서 정규 분포의 확률 밀도를 계산한다.
import numpy as np
import seaborn as sns
from scipy import stats
from matplotlib import pyplot as plt
mu = 0
sigma = 1
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
y = 100* stats.norm.pdf(x, mu, sigma)
fig, axes = plt.subplots(1, 2, figsize=(15, 5)) # subplot 생성 row=1, cols=2
sns.lineplot(x=x,y=y, color='black', ax=axes[0]) # [0] 인덱스에 선그래프
sns.lineplot(x=x,y=y, color='black', ax=axes[1]) # [1] 인덱스에 선그래프
axes[0].set_frame_on(False) # 그래프의 배경테두리 삭제
axes[1].set_frame_on(False)
axes[0].get_yaxis().set_visible(False) # 그래프의 y축 삭제
axes[1].get_yaxis().set_visible(False)
axes[0].get_xaxis().set_visible(False) # 그래프의 x축 삭제
axes[1].get_xaxis().set_visible(False)
axes[0].axhline(y=0, color='black') # y축 수평선 (y=0)
axes[0].axvline(x=mu, color='black', linestyle='--') # x축 수평선 (x=mu)
axes[1].axhline(y=0, color='black') # y축 수평선 (y=0)
axes[1].axvline(x=mu + sigma, color='black', linestyle='--') # x축 수평선 (x=mu + sigma)
axes[0].hlines(y=23.6, xmin = mu-sigma, xmax = mu, color='black')
axes[1].hlines(y=23.6, xmin = mu-sigma, xmax = mu, color='black')
axes[0].text(mu,42, r'$\mu = \mu_0$', size=20, ha="center") # 위치 지정하여 text 삽입
axes[1].text(mu + sigma, 42, r'$\mu \neq \mu_0$', size=20, ha="center")
axes[0].text(mu-sigma - 0.2, 23.6, r'$\sigma = \sigma_0$', size=20, ha="right")
axes[1].text(mu-sigma - 0.2, 23.6, r'$\sigma = \sigma_0$', size=20, ha="right")
plt.show()
- 위 그림이 의미하는 것이 바로 두 가지 전제조건을 말한다.
- ① 양쪽 모두 분포는 동일하다. ② 표준편차도 동일하다.
- 다만, 모집단의 평균과 추출된 샘플링된 평균은 같으냐? 다르냐?
3-5-2. z-score
- 각 데이터 값이 평균으로부터 얼마나 떨어져 있는지를 나타내는 통계적인 예측값
- 표준화된 수치(Standardized Score)
grades = df['grades']
sample_mean = statistics.mean(grades)
sample_mean
sd_true = 9.5
mu_null = 67.5
N = len(grades)
# 평균의 표준오차 구하기
import math
sem_true = sd_true / math.sqrt(N)
sem_true
# 2.1242645786248002
## z_score 구하기
z_score = (sample_mean - mu_null) / sem_true
z_score
# 2.259605535157681- 위 통계량이 의미하는 것은 무엇인가? 를 생각해 보자.
- 이때 아래 그래프가 필요하다.
mu = 0
sigma = 1
x = np.arange(-3,3,0.001)
y = stats.norm.pdf(x, mu, sigma)
fig, (ax0, ax1) = plt.subplots(1, 2, sharey = True, figsize=(15, 5))
# Two-sided test
crit = 1.96
p_lower = x[x<crit*-1]
p_upper = x[x>crit]
ax0.plot(x, y)
ax0.fill_between(p_lower, 0, stats.norm.pdf(p_lower, mu, sigma),color="none",hatch="///",edgecolor="b")
ax0.fill_between(p_upper, 0, stats.norm.pdf(p_upper, mu, sigma), color="none",hatch="///",edgecolor="b")
ax0.set_title("Two sided test", size = 20)
ax0.text(-1.96,-.03, '-1.96', size=18, ha="right")
ax0.text(1.96,-.03, '1.96', size=18, ha="left")
ax0.text(z_score, 0, 'O', size=18, ha="left", color = 'red')
# One-sided test
crit = 1.64
p_upper = x[x>crit]
ax1.plot(x, y)
ax1.set_title("One sided test", size = 20)
ax1.text(1.64,-.03, '1.64', size=18, ha="left")
ax1.fill_between(p_upper, 0, stats.norm.pdf(p_upper, mu, sigma), color="none",hatch="///",edgecolor="b")
ax0.set_frame_on(False)
ax1.set_frame_on(False)
ax0.get_yaxis().set_visible(False)
ax1.get_yaxis().set_visible(False)
ax0.get_xaxis().set_visible(False)
ax1.get_xaxis().set_visible(False)
plt.show()
- z-score(여기서는 2.259)가 의미하는 것은 위 분포에서 검정하려는 값이 어디에 속하는지 표현해 주는 것이다.
- 그런데, p-value를 구하려면 어떻게 해야 할까?
# P-value 구하기
from statistics import NormalDist
lower_area = NormalDist().cdf(-z_score)
upper_area = lower_area
p_value = lower_area + upper_area
p_value
# 0.023845743764939864- NormalDist(). cdf(-z_score)
- NormalDist() : 기본적으로 평균이 0이고 표준편차가 1인 정규 분포 개체를 생성
- .cdf() : 확률 변수 X가 주어진 값보다 작거나 같을 확률을 알려준다.
- .cdf() 메서드는 주어진 값에서 정규 분포의 누적 분포 함수(CDF)를 계산하는 데 사용. 이 경우 입력 값은 -z_score
- z_score가 음수이면 x가 평균보다 낮고, z_score가 양수이면 x가 평균보다 높다고 볼 수 있다.
3-6. 결론 및 정리
- p-value가 0.02라는 값은, 귀무가설을 기각하고, 대립가설을 채택해야 한다는 것을 의미한다.
- 즉, 표본평균이 모집단의 평균과 같지 않음을 의미.
4. One-Sample T-test
- z-test와 t-test의 가장 큰 차이점
- z-test: 모수의 표준편차를 안다
- t-test : 모수의 표준편차를 모른다.
- 이것이 의미하는 것은 샘플의 표준편차를 여러 번 구해서 모수의 표준편차를 추정(estimate)하는 것이다.
4-1. 샘플 표준편차 구하기
# 데이터 불러오기
import pandas as pd
df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/zeppo.csv")
# 샘플의 표준편차 구하기
import statistics
statistics.stdev(df['grades'])
# 9.520614752375915- 샘플의 표준편차(σ^)는 9.52라고 말할 수 있다.
- 그러나, 모집단의 표준편차(σ)는 9.5라고 말할 수 없다.
- 앞서 했던 Z-TEST에서는 모수의 표준편차를 아는 조건이 있었지만, T-TEST는 모수의 표준편자를 모르는 상태로 추정하는 것이다.
4-2. 가설 검정
4-2-1. 가설의 전제조건
- 기본적으로 z-test와 동일
- 샘플은 정규분포를 이루고 있다. (정규성(Normality))
- 샘플의 관측값은 서로 독립적으로 생성됨 (독립성(Independence))
- 모수의 표준편차를 알지 못한다.
4-2-2. 가설 설정
- 귀무가설(H0) : 모집단의 평균은 100이다.
- 대립가설(H1) : 모집단의 평균은 100이 아니다
# 모수의 표준편차를 모를 때, 모수와 샘플의 평균 비교 판단
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import scipy.stats as stats
mu = 0 # 평균
sigma = 1 # 표준편차
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
y = 100 * stats.norm.pdf(x, mu, sigma)
fig axes = plt.subplots(1, 2, figsize = (15, 5))
sns.lineplot(x = x, y = y, color = 'black', ax = axes[0]
sns.lineplot(x = x, y = y, color = 'black', ax = axes[1]
axes[0].set_frame_on(False)
axes[1].set_frame_on(False)
axes[0].get_yaxis().set_visible(False)
axes[1].get_yaxis().set_visible(False)
axes[0].get_xaxis().set_visible(False)
axes[1].get_xaxis().set_visible(False)
axes[0].axhline(y = 0, color = 'black')
axes[0].axvline(x = mu, color = 'black', linestyle = '--')
axes[1].axhline(y = 0, color = 'black')
axes[1].axvline(x = mu + sigma, color = 'black', linestyle = '--')
axes[0].hlines(y = 23.6, xmin = mu - sigma, xmax = mu, color = 'black')
axes[1].hlines(y = 23.6, xmin = mu - sigma, xmax = mu, color = 'black')
axes[0].text(mu, 42, r'$\mu = \mu_0$', size = 20, ha = 'center')
axes[1].text(mu + sigma, 42, r'$\mu \neq \mu_0$', size = 20, ha = 'center')
axes[0].text(mu - sigma - 0.2, 23.6, r'$\sigma = ??$', size = 20, ha = 'right')
axes[1].text(mu - sigma - 0.2, 23.6, r'$\sigma = ??$', size = 20, ha = 'right')

4-2-3. 추정
- 모수에서 추출한 Sample의 평균은 구했지만, 전체 모수를 추정할 수 있을까?
- 샘플 수를 늘려보면 좀 더 정확해진다.
# Sample 수에 따른 분포 비교
mu = 0 # 평균
variance = 1 # 분산
sigma = np.sqrt(variance) # 표준편차
x = np.linspace(-4, 4, 100) # x축 설정 (min, max, divide)
y_norm = stats.norm.pdf(x, mu, sigma) # 분포 생성
fig, axes = plt.subplots(1, 2, figsize=(15, 5))
# 자유도가 2일 때의 T-분포 (점선)
y_t = stats.t.pdf(x, 2)
sns.lineplot(x = x, y = y_norm, color = 'black', linestyle='--', ax = axes[0])
sns.lineplot(x = x, y = y_t, color = 'black', ax = axes[0])
# 자유도가 10일 때의 T-분포 (점선)
y_t = stats.t.pdf(x, 10)
sns.lineplot(x = x, y = y_norm, color = 'black', linestyle='--', ax = axes[1])
sns.lineplot(x = x, y = y_t, color = 'black', ax = axes[1])
axes[0].text(0, 0.42, r'$df = 2$', size=20, ha="center")
axes[1].text(0, 0.42, r'$df = 10$', size=20, ha="center")
# sns.despine()
axes[0].get_yaxis().set_visible(False)
axes[1].get_yaxis().set_visible(False)
axes[0].set_frame_on(False)
axes[1].set_frame_on(False)
plt.show()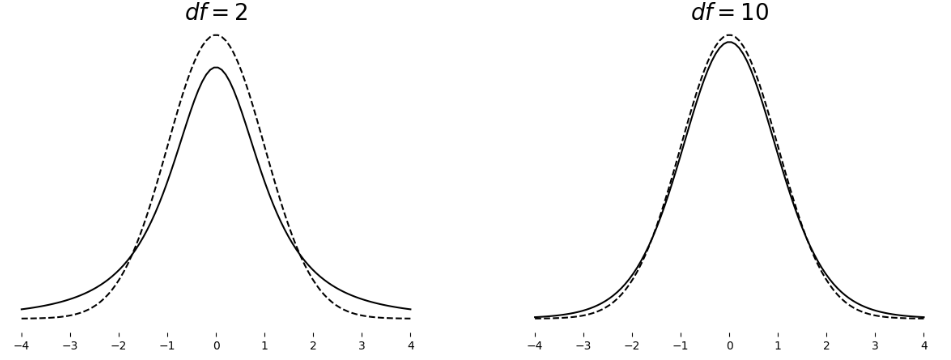
- 그림 해석
- df는 자유도(Degrees of Freedom)를 의미한다. 자유도란 Sample의 개수 N에서 -1을 한 값이다.
- df가 커질수록 이상적인 분포(실선)와 가까워진다. >> 중심극한정리 참고
- 즉, 모수 대비 Sample의 개수가 커질수록 모수를 추정하는 정확도 또한 올라간다.
5. One-Sample t-test 예제 실습
5-1. 전제 조건
- 전국 대학생의 평균 점수는 67.5이다.
- 우리 대학생 20명의 평균은 00이다.
5-2. 가설 설정
- 귀무가설(H0) : 전국 대학생의 평균 점수와 우리 대학생의 평균점수는 통계적으로 유의하게 같다.
- 대립가설(H1) : 전국 대학생의 평균 점수와 우리 대학생의 평균점수는 통계적으로 유의하게 다르다.
5-3. 가설 검정
5-3-1. t 통계량, p-value 값 구하기
from scipy.stats import ttest_1samp
t, p = ttest_1samp(a = df['grades'], popmean = 67.5)
t, p
# (2.25471286700693, 0.03614521878144544)5-3-2. 표본의 평균, 자유도 구하기
N = len(df['grades'])
degfree = N-1
sample_mean = statistics.mean(df['grades'])
print('Sample의 평균 : ', sample_mean)
print('자유도 : ', degfree)
# Sample의 평균 : 72.3
# 자유도 : 195-3-3. 신뢰구간 구하기
from scipy import stats
confidence_level = 0.95
degrees_freedom = len(df['grades'])-1
sample_mean = statistics.mean(df['grades'])
sample_standard_error = stats.sem(df['grades'])
confidence_interval = stats.t.interval(confidence_level, degrees_freedom,
sample_mean, sample_standard_error)
confidence_interval
# (67.84421513791415, 76.75578486208585)5-4. 결론 및 정리
- 평균 72.3을 기록한 우리 학생들의 평균 점수는 전체 대학생의 평균점수 67.5보다 약간 높다.
- t(19)=2.25, p<0.05, 신뢰도 95% 신뢰구간=[67.8,76.8]
6. pingouin 라이브러리 소개
- pandas와 numpy를 기반으로 한 오픈소스 통계 패키지이다.
- 자세한 기능은 https://pingouin-stats.org/build/html/index.html 에서 확인하기 바란다.
!pip install --upgrade pingouin
from pingouin import ttest
ttest(df['grades'], 67.5)
7. 마치며
이것으로 One-Sample에 대한 Z-TEST & T-TEST에 대해 알아보았다.
Z-TEST는 실생활에서는 거의 쓰이지 않지만 이번에 배운 내용을 바탕으로 한 단계씩 더 나아가 실무에서도 T-TEST를 사용할 수 있기를 바란다.
다음에는 Independent_Sample T-test(독립표본 t-test), Paired_Sample T-test(대응표본 t-test)에 대해서 다뤄 보겠다.
다음 글
[Python 통계 분석 실습] 2. Independent-Sample(독립표본) T-TEST
[Python 통계 분석 실습] 3. Independent-Sample(독립표본) T-TEST의 비모수적 검정
728x90
반응형
'Python > 실습' 카테고리의 다른 글
| [Python 통계 분석 실습] 2. Independent-Sample(독립표본) T-TEST (0) | 2023.04.30 |
|---|---|
| [Python Streamlit] IRIS 데이터를 활용한 머신러닝 대시보드 개발 (2) | 2023.04.25 |